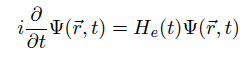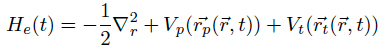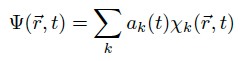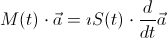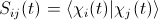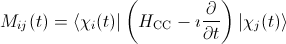AOCC calculations

contact: Dipl.-Ing. Katharina Igenbergs, Prof. Dr. Friedrich Aumayr

In collaboration with J. Schweinzer from IPP Garching state selective single electron capture cross sections between multiply charged ions and atomic hydrogen atoms are calculated on the basis of an Atomic Orbital Close Coupling code (AOCC). Such cross sections are needed for diagnostics of fusion plasmas via charge exchange recombination spectroscopy using fast hydrogen/deuterium (diagnostic or heating) beams.

To model the dynamics of a plasma, one must understand the charge exchanges resulting from the collision of its particles. Unfortunately, this quantum-mechanical three-body problem (two collision partners and the electron in question) in general cannot be solved analytically. As a result, a wide array of numerical methods have been derived to estimate these cross sections. The close-coupling method is one of the most successful methods and was repeatedly used to predict charge exchange cross sections with good accuracy.

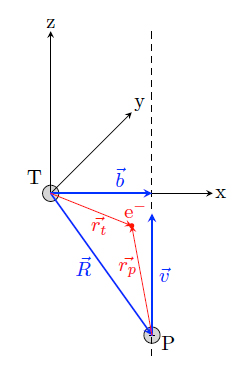The close-coupling formalism provides a semi-classical description of a collisional process. The motion of the cores are calculated on classical trajectories, whereas the electron movement is calculated quantum mechanically. The figure on the right shows the collision frame and geometry in the impact parameter approximation: the (x,z) collision plane is defined by the projectile velocity v and the target. b is the impact parameter, R the internuclear separation vector, and r _t and r _p the position vectors of the active electron the coordinate system of the target (T) respectively the projectile (P).

From the figure it is clear that the nuclei not only move on classical trajectories, but we also neglect coulomb scattering of the nuclei. This simplification is justified for high impact velocities v > 1 keV or big impact parameters b. The equation of motion of the active electron in the effective potential of the target core respectively the projectile core is described by the time-dependent Schrödinger equation

where we again neglected any quantum-mechanical dynamics from the nuclei (Close-coupling Hamiltonian). We start out by expanding the electronic wavefunctions into a finite set of basis functions χ_k

thus considering only a finite linear subspace of the full Hilbert space of the problem. Now an optimal description of the collisional process in question needs to be found, which relates to choosing 'good' basis functions for the problem. This is highly non-trivial and no canonical way to select basis function has been found yet. However, it turned out that three types of basis function provided good agreement with the experiments:

• Atomic orbitals (AO), which are bound states on either centre provide the 'bread-and-butter'-states for the CC-method, because they model the behaviour of the system at infinite separation.
• Molecular orbitals (MO), which are states on the union of both centres model the intermediate behaviour at low energies well.
• United atoms (AO+), are non-bound states on either centre, which correspond to the capture of the electron into the continuum.

The expansion above transforms the Schrödinger equation for the wavefunction Ψ into a matrix equation for the amplitude vector a:

M and S are time-dependent matrices. S is commonly called overlap matrix and comes from the fact that we are usually forced to choose a non-orthogonal basis. It encapsulates the overlap of the different basis states on different centres:

The coupling matrix M, on the other hand, refers to the “real” time dependence of the system, namely the action of the close-coupling Hamilton operator on the basis states. Unlike the overlap matrix S it is not Hermitian because of the inclusion of the intrinsic time dependence of the non-orthogonal basis states:

This matrix differential equation, or perhaps more precisely, the initial value problem for a set of coupled linear differential equations, is a very common task in computational physics and numerics in general. A vast set of solvers are available for these so-called ordinary differential equations (ODEs). Most of these solvers start from an intial value and integrate the equations in small but finite steps, yielding an approximate solution (an “accurate” solution would be if we took infinitely many infinitely small steps).

In physical terms, they start with an initial population of the channels at time t, given by the amplitude vector a. Then they compute the interaction of the channels at this time through the matrices M and S. They then use this information to re-distribute the population of the channels at a time t + Δt, taking a time step of Δt.